初识动态规划

简单的认识

动态规划实际上是一个暴力求解的过程，举个例子：斐波那契数列，0、1、1、2、3、5、8……斐波那契数列其中一项的值就是由前两项相加得出的，那么0+1=1，1+1=2，1+2=3，2+3=5，3+5=8这个过程，实际上就是“动态规划的过程”

动态规划如何解题

动态规划的解题步骤

  1. 确定dp数组以及下标的含义
  2. 确定递推公式
  3. dp数组如何初始化
  4. 确定遍历顺序
    注：我们在做题的过程要始终记得dp数组的含义，不然很容易混乱。

尝试应用方法

做点简单题

我们先看这道题

70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
示例 1：

输入：n = 2
输出： 2
解释：有两种方法可以爬到楼顶。

  1. 1 阶 + 1 阶
  2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

  1. 1 阶 + 1 阶 + 1 阶
  2. 1 阶 + 2 阶
  3. 2 阶 + 1 阶
  • 第一步：我们先确定dp数组含义，即：dp[n]：上第n个台阶有dp[n]种方法。
  • 第二步：确定递推公式，我们可以分析一下：
    第一个台阶，一种方式（迈一步）
    第二个台阶，两种方式（迈一步2次，迈两步1次）
    第三个台阶，三种方式（迈一步3次，迈一步再迈两步，迈两步再迈一步）
    ……
    这时我们发现规律：想上第三个台阶，可以拆分成第一个台阶迈两步和第二个台阶迈一步，所以我们得出结论：第三个台阶方法数=第一个台阶方法数加第二个台阶方法数，即dp[3]=dp[2]+dp[1]，则递推公式为：dp[n]=dp[n-1]+dp[n-2]
  • 第三步：第一个台阶是一种方式即dp[1]=1，第二个台阶即dp[2]=2，那么我们初始化dp[0]=1。
  • 第四步：这个题比较简单，遍历顺序一下就看出来了：从低往高处走,i从小到大 。

那么我们写出代码：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {     //注意从dp[2]开始
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

我们再做一个差不多的题目感受一下。

746. 使用最小花费爬楼梯

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。

  • 支付 15 ，向上爬两个台阶，到达楼梯顶部。
    总花费为 15 。
    示例 2：

输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。

  • 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。

  • 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。

  • 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。

  • 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。

  • 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。

  • 支付 1 ，向上爬一个台阶，到达楼梯顶部。
    总花费为 6 。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    class Solution {  
        public int minCostClimbingStairs(int[] cost) {  
            int n = cost.length;  
            if (n < 2) return cost[0];  
            if (n < 3) return Math.min(cost[0], cost[1]);  
            int[] dp = new int[n];  
            dp[0] = cost[0];  
            dp[1] = cost[1];  
            for (int i = 2; i < n; i++) {  
                dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];  
            }  
            return Math.min(dp[n - 1], dp[n - 2]);  
        }  
    }

  • 第一步：我们先确定dp数组含义，即：dp[n]：上第n个台阶最少消费dp[n]的钱。

  • 第二步：确定递推公式，第n个台阶等于第n-1个台阶和第n-2个台阶的最小值加上自己的消费，则递推公式为：dp[n]=dp[n-1]+dp[n-2]+cost[n]

  • 第三步：第一个台阶的消费是cost[0],第二个台阶的消费是cost[1]。

  • 第四步：从低往高处走 ，即从dp[0]到dp[n]。
    这个题要注意最后我们要选择倒数第一和倒数第二的台阶中的最小值。

提高难度

62. 不同路径

方法一：

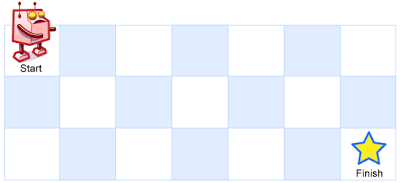
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？
示例 1：

输入

输入：m = 3, n = 7
输出：28
示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

  1. 向右 -> 向下 -> 向下
  2. 向下 -> 向下 -> 向右
  3. 向下 -> 向右 -> 向下
    示例 3：

输入：m = 7, n = 3
输出：28
示例 4：

输入：m = 3, n = 3
输出：6

  • 第一步：我们先确定dp数组含义，即：dp[m][n]：到mn位置有dp[m][n]种路径
  • 第二步：确定递推公式，因为只能往下，往右走，可以得知，dp[i][j]由它左边和上边推测得到，则递推公式为：dp[i][j]=dp[i][j-1]+dp[i-1][j]

  • 第
  • 第三步：我们可以想象一下，第一行因为只能从左边走，所以都只有1种路径。因此第一行第一列都为1。
  • 第四步：先从左往右，再从上到下，也可以先从上到下，再从左到右。在这道题里是没区别的。此时，这个遍历顺序就开始要注意一下了，因为有的题可能其中一种顺序才能做出来或者更好写，甚至有的时候需要从右到左才行，我们要知道这个顺序是怎么来的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//方法一
class Solution {  
    public int uniquePaths(int m, int n) {  
        if (m == 1 || n == 1) return 1;  
        int[][] dp = new int[m][n];  
        for (int i = 0; i < m; i++) {  
            dp[i][0] = 1;  
        }  
        for (int i = 0; i < n; i++) {  
            dp[0][i] = 1;  
        }  
        for (int i = 1; i < m; i++) {  
            for (int j = 1; j < n; j++) {  
                dp[i][j] = dp[i][j - 1] + dp[i - 1][j];  
            }  
        }  
        return dp[m - 1][n - 1];  
    }  
}

方法二：
我们注意到遍历顺序，是先按照从左到右，然后从上到下的顺序来的，每次dp[i][j]都会由它上边和左边得到，所以每当我们计算完一行数据，它的上一行数据是作废的（左边数据不会作废，因为下一行计算还需要），那么我们就可以使用一个一维数组来进行求解，这样可以减少空间复杂度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {  
    public int uniquePaths(int m, int n) {  
        if (m == 1 || n == 1) return 1;  
        int[] dp = new int[n];  
        for (int i = 0; i < n; i++) {  
            dp[i] = 1;  
        }  
        for (int i = 1; i < m; i++) {  
            for (int j = 1; j < n; j++) {  
                dp[j] = dp[j] + dp[j - 1]; //dp[j]指的是上一行的数据，dp[j-1]指的是左边的数据 
            }  
        }  
        return dp[n - 1];  
    }  
}

dp[j] = dp[j] + dp[j - 1]; //等号右边：dp[j]指的是上一行的数据，dp[j-1]指的是左边的数据

63. 不同路径 II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1：

Pasted image 20241024190606

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

  1. 向右 -> 向右 -> 向下 -> 向下
  2. 向下 -> 向下 -> 向右 -> 向右
    示例 2：

Pasted image 20241024190616
输入：obstacleGrid = [[0,1],[0,0]]
输出：1

这道题只是比上一道多了一个判断障碍物，我们只需注意两点：

  • 初始化的时候如果第一行或第一列有障碍物，那么障碍物之后的路径数都为0
  • 遍历其他地方，如果出现障碍物，那么该位置的路径数为0
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    //方法一
    class Solution {  
        public int uniquePathsWithObstacles(int[][] obstacleGrid) {  
            int m=obstacleGrid.length;  
            int n=obstacleGrid[0].length;  
            if (obstacleGrid[0][0] == 1) {  
                return 0;  
            }  
            int[][] dp = new int[m][n];  
            dp[0][0] = 1;  
            for (int i = 1; i < m; i++) {  
                dp[i][0] = (obstacleGrid[i][0] == 1) ? 0 : dp[i - 1][0]; //障碍物之后都设为0 
            }  
            for (int j = 1; j < n; j++) {  
                dp[0][j] = (obstacleGrid[0][j] == 1) ? 0 : dp[0][j - 1];  
            }  
            for (int i = 1; i < m; i++) {  
                for (int j = 1; j < n; j++) {  
                    if (obstacleGrid[i][j] == 1) {  //判断是否是障碍物
                        dp[i][j] = 0;  
                    } else {  
                        dp[i][j] = dp[i - 1][j] + dp[i][j - 1];  
                    }  
                }  
            }  
            return dp[m - 1][n - 1];  
        }  
    }

方法二需要注意一点：与之前不同的是，之前没有障碍物，那么第一个元素永远为1，现在有可能第一列有障碍物，那么我们没遍历完一行，需要判断下一行第一个是否是障碍物，及时更改dp[0]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//方法二
class Solution {  
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {  
        int m = obstacleGrid.length;  
        int n = obstacleGrid[0].length;  
        if (obstacleGrid[0][0] == 1) {  
            return 0;  
        }  
        int[] dp = new int[n];  
        dp[0] = 1;  
        for (int j = 1; j < n; j++) {  
            dp[j] = (obstacleGrid[0][j] == 1) ? 0 : dp[j - 1];  
        }  
        for (int i = 1; i < m; i++) {  
            dp[0] = (obstacleGrid[i][0] == 1) ? 0 : dp[0]; //判断第一列是否有障碍物
            for (int j = 1; j < n; j++) {  
                if (obstacleGrid[i][j] == 1) {  
                    dp[j] = 0;  
                } else {  
                    dp[j] = dp[j] + dp[j - 1];  
                }  
            }  
        }  
        return dp[n - 1];  
    }  
}